CHAPTER 3 | IMPOSSIBLE FIGURES

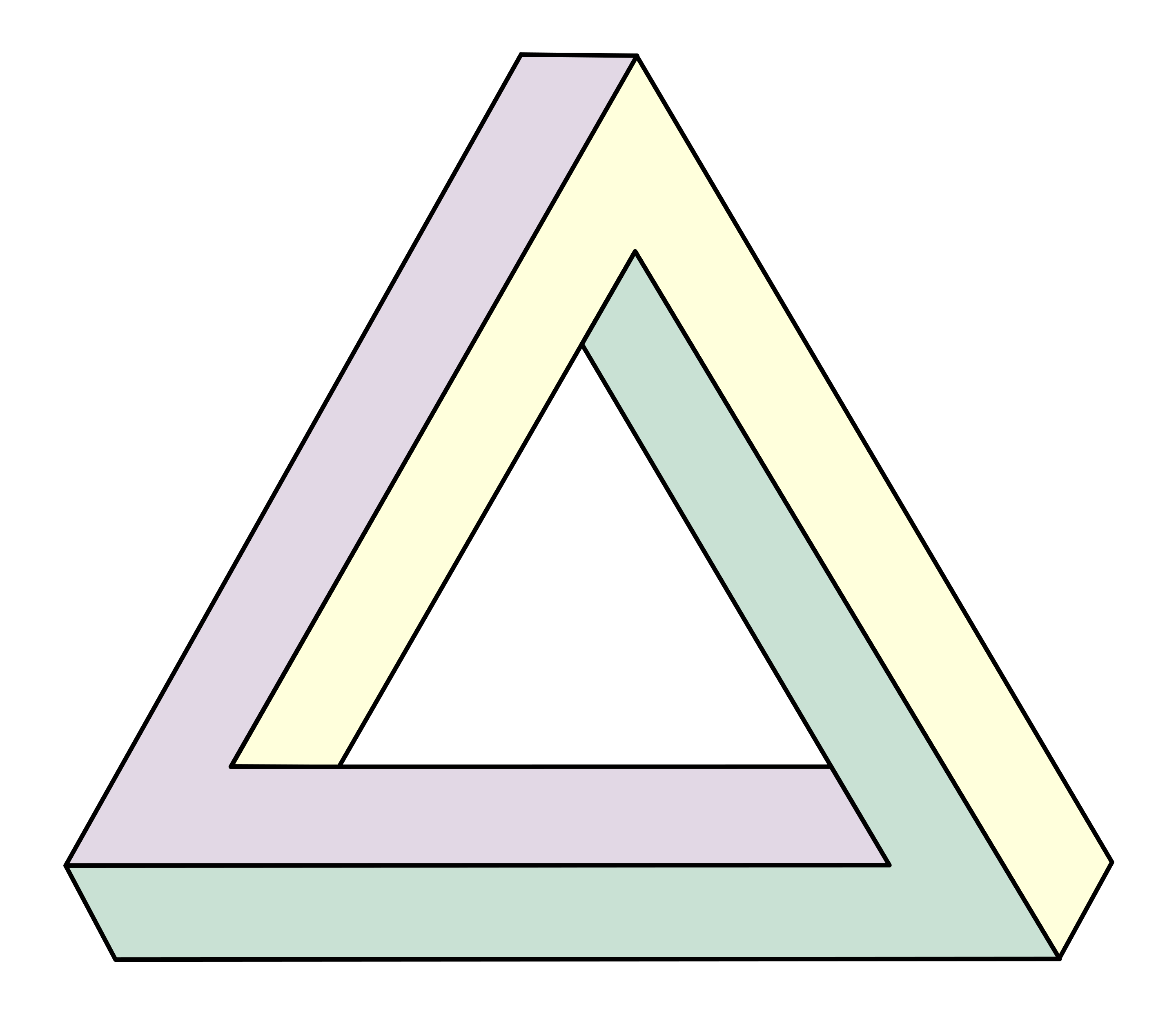
The figures in this lesson cannot possibly exist in three dimensions. It is a form of optical illusion. The most famous example is the impossible triangle, originally drawn by the Swedish artist Oscar Reutersvärd as early as 1934. It’s remarkable that he had great difficulty as a child estimating dimensions and distances. In 1958, the triangle became world famous as it was reinvented by the mathematician and physicist Roger Penrose. The Penrose triangle continues to appear in all sorts of (also digital) variations.

Exercise 1: Watch the video and try to draw an impossible triangle yourself. If you want it to do it neater, use a ruler after the light sketch. You can always add anything you like.

The Penrose triangle continues to appear in all sorts of (also digital) variations. With three added shades of gray and a standing figure, the triangle becomes more spatial. In a still from the stunningly beautiful game Monument Valley, the triangle forms part of an Escher-esque structure.

Exercise 2: There are of course more impossible figures. Draw all three figures from the following two rows. The left figure is flat/geometric, the middle one is perfectly 3D, and the right one is… impossible. An eraser is definitely not superfluous.

A special case is the so called devil’s (tuning) fork. If you cover the three circles, it suddenly has only two legs. Because of its ambiguous shape, it appeared on the cover of the comic magazine MAD in 1965. You can see from the double eyes of the laughing figure that he doesn’t understand anything either.

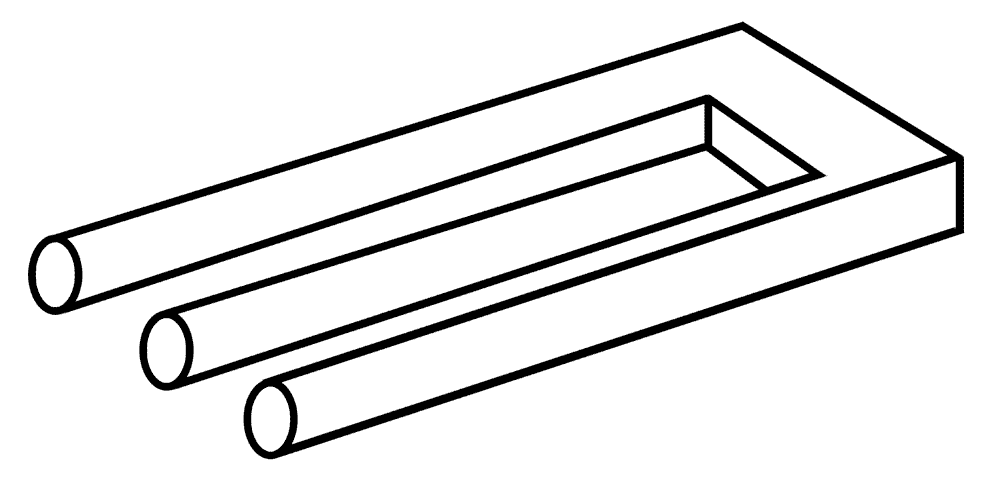
The following drawing of a candelabrum (or candlestick) is based on the devil’s fork. If you cover the three candle flames in the impossible figure on the right, the candlestick has only two legs. In fact, the middle two drawings are also impossible because the candles at the top look 3D and at the bottom flat.

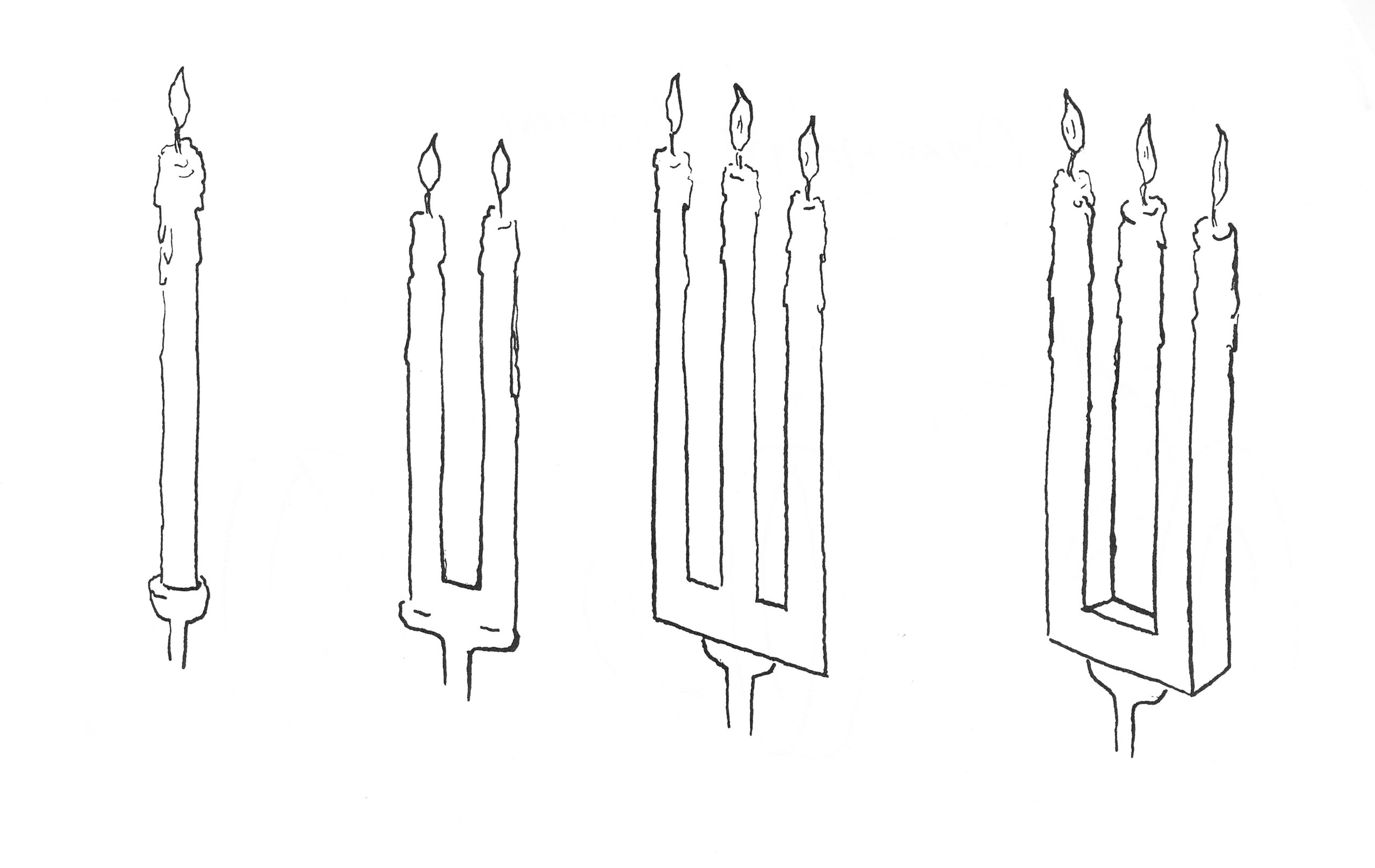
Exercise 3: draw the rightmost candelabrum with the three candles.