HOOFDSTUK 3 | ONMOGELIJKE FIGUREN
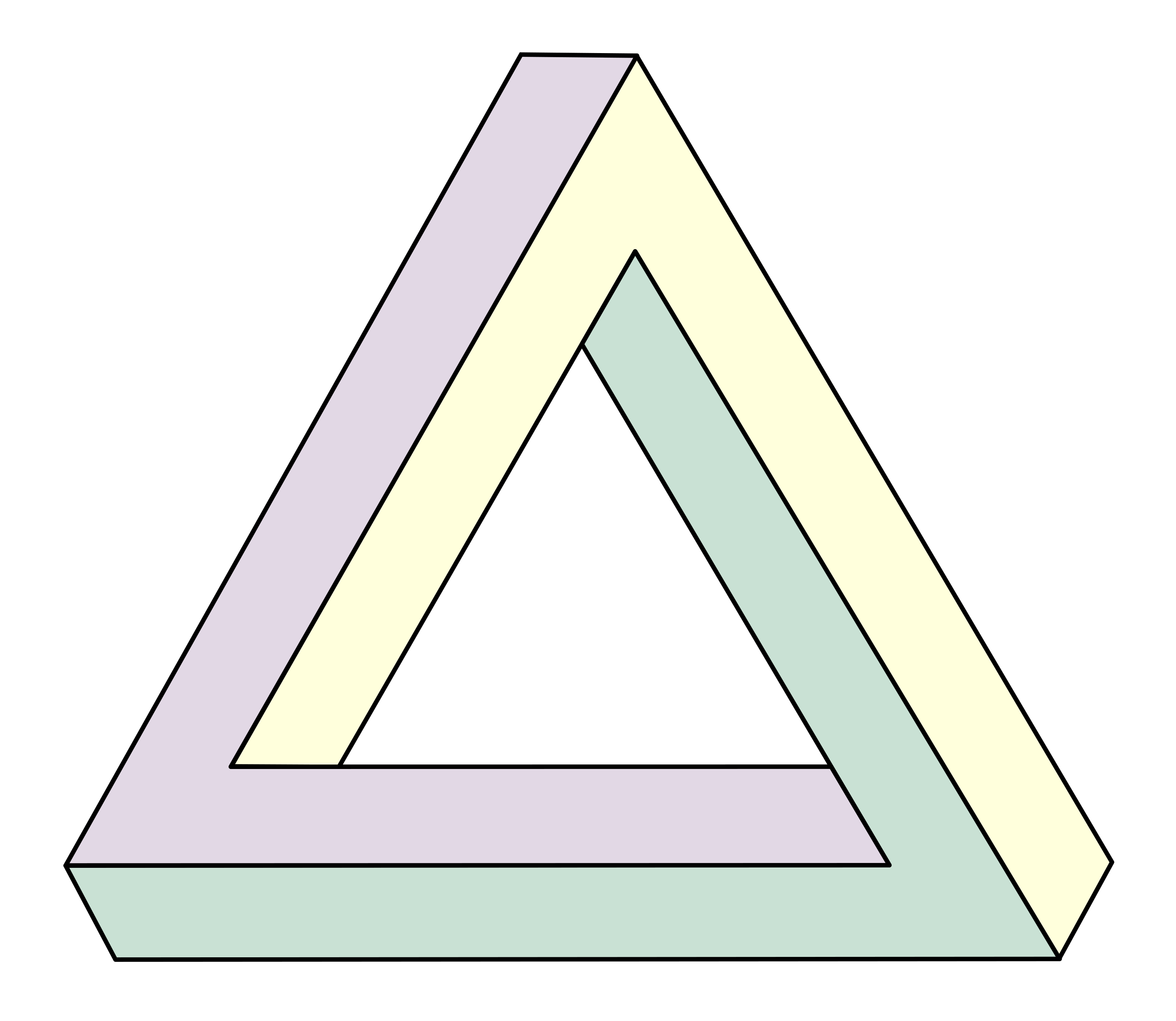
De figuren in deze les kunnen onmogelijk in drie dimensies bestaan. Het is een vorm van gezichtsbedrog. Het beroemdste voorbeeld is de onmogelijke driehoek, al in 1934 getekend door de Zweedse kunstenaar Oscar Reutersvärd. Het is opmerkelijk dat hij als kind juist moeite had met het schatten van afmetingen en afstanden. In 1958 werd de driehoek wereldberoemd toen deze opnieuw werd uitgevonden door de wis- en natuurkundige Roger Penrose. De Penrose-driehoek duikt nog steeds op in allerlei ook digitale variaties.

Oefening 1: Bekijk de video en probeer zelf zo’n onmogelijke driehoek te tekenen. Als je het graag strakker wil tekenen gebruik je na de lichte opzet een liniaal. Je kan er altijd van alles bij verzinnen.
In een still uit de weergaloos mooie game Monument Valley vormt de driehoek een onderdeel van een Escher-achtig bouwsel

Oefening 2: Zo zijn er meer onmogelijke figuren. Teken van de volgende twee rijtjes alle drie de figuren. De linker figuur is vlak/geometrisch, de middelste is kloppend 3D en de rechter is … onmogelijk. Een gummetje is zeker niet overbodig.

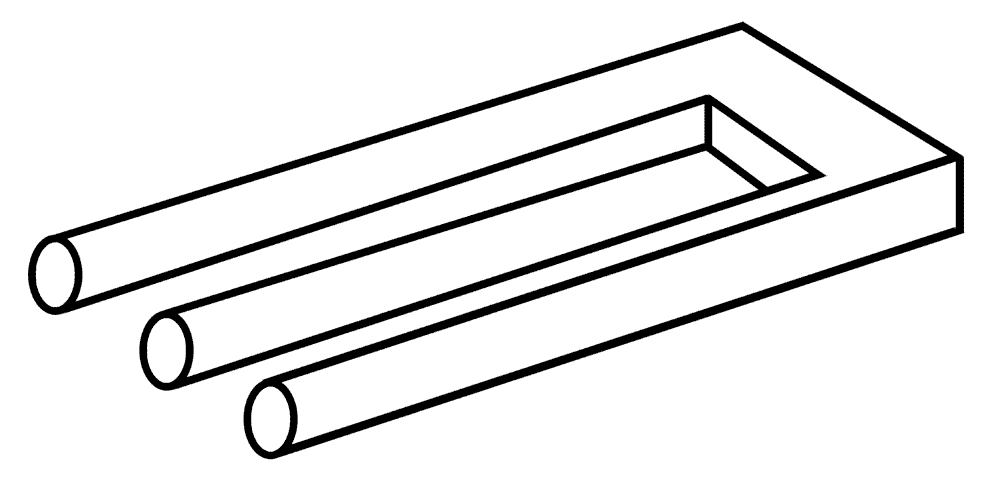
Een apart geval is de zogenaamde duivels(stem)vork. Als je de drie cirkels bedekt heeft hij ineens maar twee poten. Vanwege deze dubbelzinnige vorm verscheen hij zelfs op de omslag van een komisch tijdschrift MAD. Aan de dubbele ogen van de lachende figuur zie je dat hij er ook niets van begrijpt.

De volgende tekening van een kaarsenkandelaar is gebaseerd op de duivelsvork. Als je in de onmogelijke rechterfiguur de drie kaarsvlammen bedekt heeft de kandelaar ineens maar twee poten. Eigenlijk zijn ook de middelste twee tekeningen al onmogelijk omdat de kaarsen bovenin 3D zijn getekend en de aan onderkant plat.
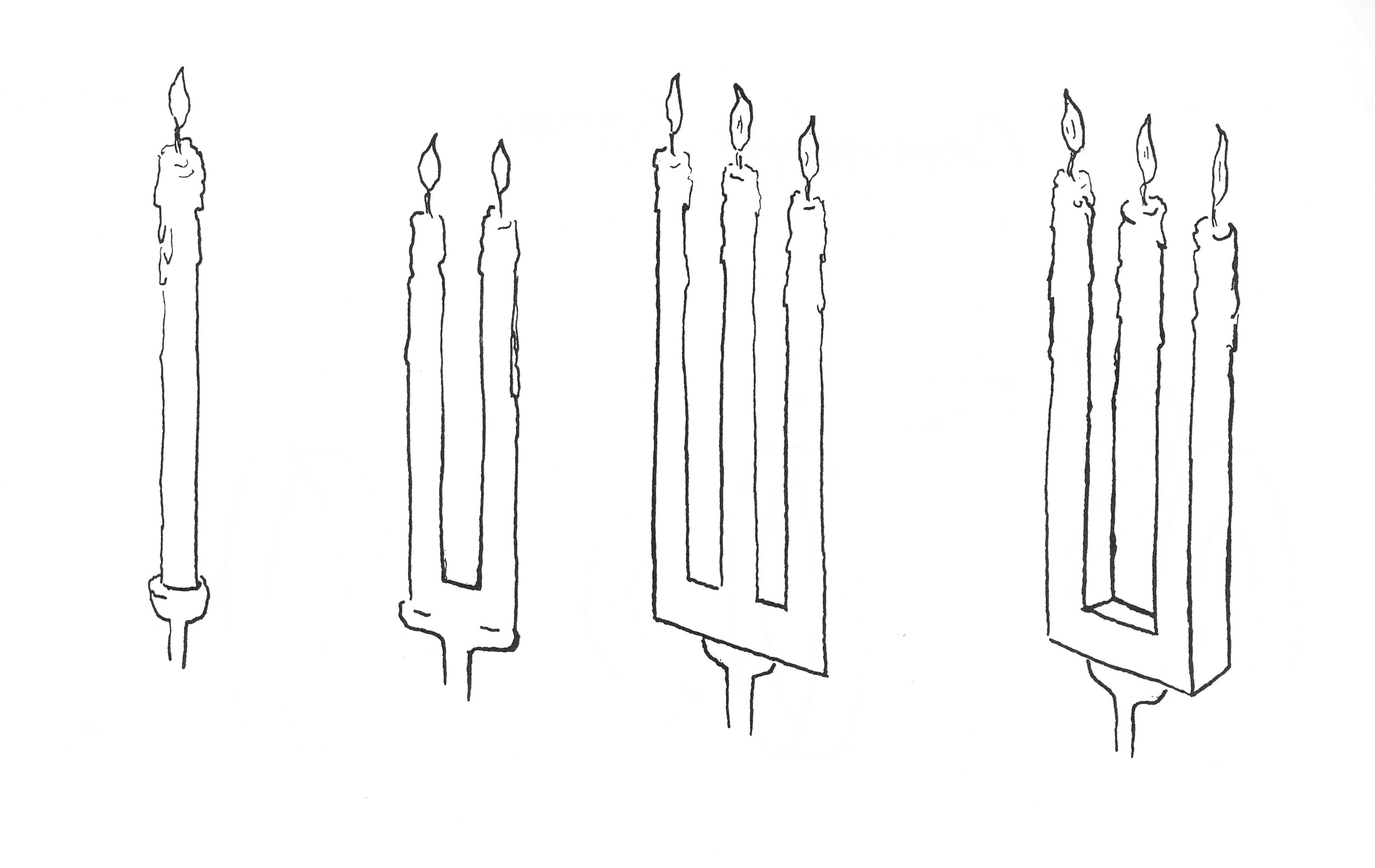
Oefening 3: teken de meest rechtse kandelaar met de drie kaarsen